Table of Contents
Introduction
Hash Table is a data structure to insert, delete and retrieve data quickly, using the concept of “Hashing”.
As we have already seen, we can do the search operations quickly using balanced binary search trees with a time complexity of O(log n).
With the help of Hashing we can reduce the “average case” complexity down to O(1) which is constant time complexity.
The worst case time complexity in “Hashing” is still O(n).
Understanding Hashing Technique using Hash Table
Let’s say we have some data e.g a string or numeric value or the combination of both. We want to store this data efficiently e.g let’s say we have
empID = ‘A001XXPP9’
So empID has an Alphanumeric value and we want to store it. Hash table provides a very unique and most efficient way to store, update, remove and access this data.
There are three main components in Hashing.
- Input Key / Key
- Hash Function
- Hash Table
Input Key is the data that we want to insert into the Hash table.
In this case it is empID ( value is ‘A001XXPP9’ ).
In the first step, we use the key ( We will use “input Key” and “key” alternatively. Both are same ) as an input parameter to a function called the hash function.
Hash Function is a simple javascript function which takes a key as input parameter and returns an index.
An index is nothing but an integer number which points to a bucket number.
We will discuss what a bucket is, so don’t get confused.
function hash( key) {
// performs some Mathematical
// operations on the key
returns index
}
const index = hash(key)
In the second step we store the key into the Hash-table.
Along with the key, we store some extra information related to that particular key ( e.g in our case employee name, employee address , employee salary etc) in the value part of the ( key , value) pair.
But before we understand how we store the key inside a Hash Table, we need to know what a Hash Table is and how we can programmatically implement it.
A Hash table is an array of buckets. Each bucket contains single or multiple (key-value) pairs, depending on our implementation style.
Implementation of the bucket is done specifically to handle collision effectively.
A collision is when for two different “key” values, the hash function generates the same index number.
However we can minimize collision occurrence and it depends on how efficiently our hash() function is implemented.
There are many different ways we can implement the hash function logic but it depends on what type of problem we are solving.
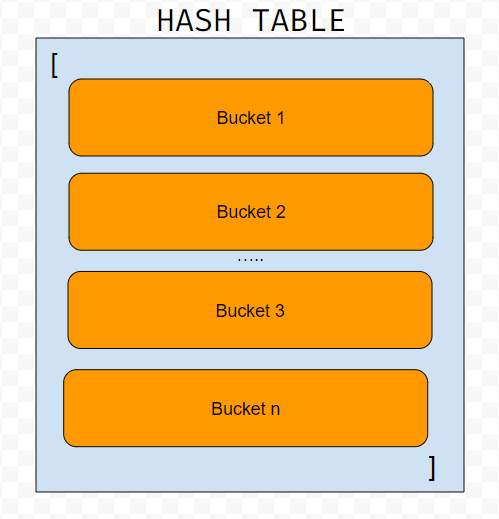
A bucket can be implemented in one of the following ways.
- A single ( key, value) pair
- Associative Array
- Array of Array
- Array of Objects
- Linked List
We can implement buckets in a very straight forward simple way or in a little complicated way.
The purpose of implementing buckets in this manner is legit. We want to handle collisions. Now what is a collision ? We will talk about that shortly.
Implementation of a bucket in a simple way.
In this type of implementation each bucket contains only one ( key, value ) pair.
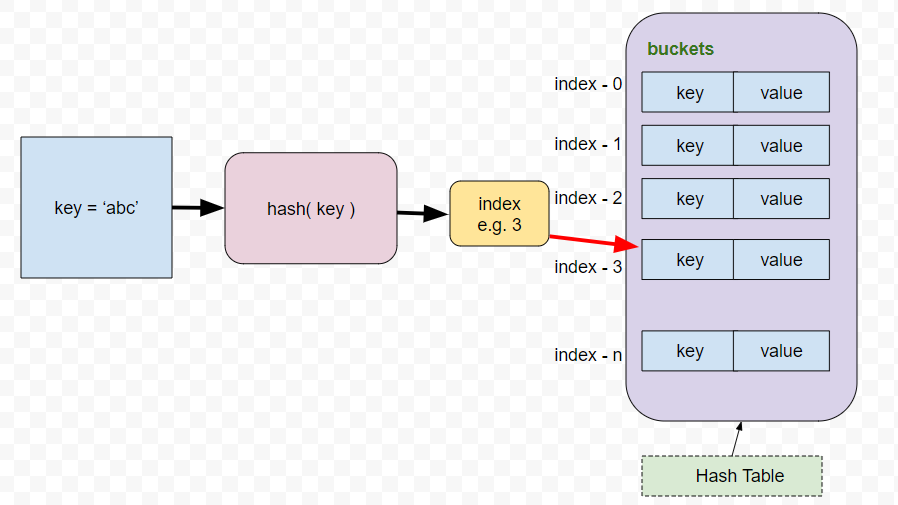
In this type of implementation, once we get the index from the hash function, we need to store the key along with some other values ( as we discussed before ) which are very specific to that key only, inside that bucket, the index of which matches with the index generated by the hash function.
Each bucket contains only one ( key, value ) pair.
Implementation of a bucket in a more complex way.
In this type of implementation, each bucket contains multiple ( key, value) pairs. So we use one of the following strategies.
- Associative Array
- Array of Array
- Array of Objects
- Linked List
But before going into depth, we need to have a clear understanding of the following concepts.
What is an associative array?
An associative array is a data structure that stores a collection of key-value pairs.
Instead of using a numeric index like a traditional array, an associative array allows you to access elements using a unique key.
The key can be any data type, such as a string or number, and it is associated with a specific value.
In simple programming terms, an associative array is nothing but an array of objects.
let bucket = {
"Alice": 85,
"Bob": 92,
"Charlie": 88
};
console.log(studentGrades[“Bob”]); // Output: 92
Array of Objects
let bucket = [
{ key: "France", value: 111 },
{ key: "Spain", value: 150 },
]Array of Arrays
let bucket = [
["France", 111],
["Spain", 150],
]In an associative array, the keys can theoretically be of any data type, though JavaScript objects treat keys as strings. However, JavaScript’s Map provides true key flexibility, where keys can be of any data type (e.g., objects, numbers, strings).
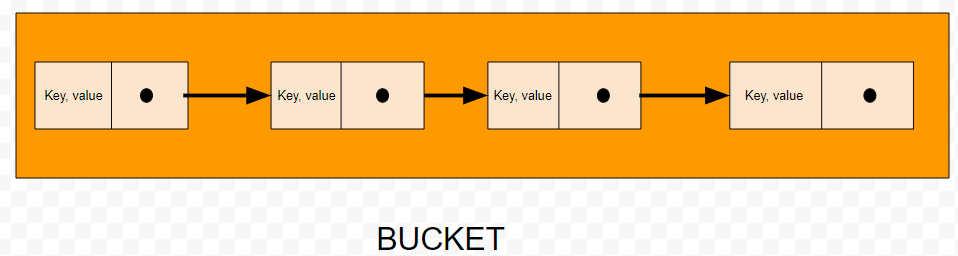
Linked List
class Node {
constructor(key, value) {
this.key = key; // The key for the key-value pair
this.value = value; // The value associated with the key
this.next = null; // Pointer to the next node (key-value pair)
}
}
How are the keys mapped to HASH TABLE ?
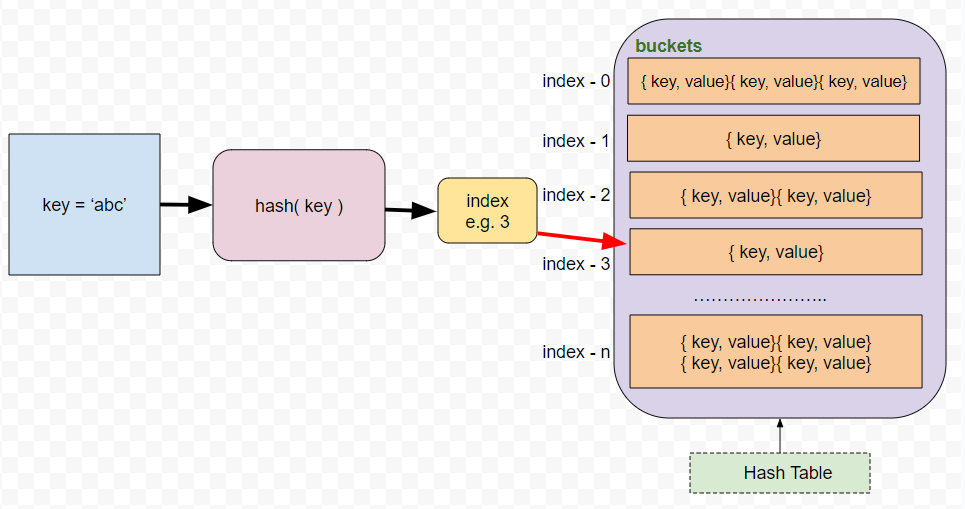
In this type of implementation, once we get the index from the hash function, we need to store the key along with some other values ( as we discussed before ) which are very specific to that key only, inside that bucket, the index of which matches with the index generated by the hash function.
Each bucket has multiple (key, value) pairs.
So a Hash Table has ‘n’ number of buckets.
Each bucket has ‘m’ number of ( key, value) pairs.
Now why do we need such a complicated structure to store data ?
Collision
Now a situation can arise where for 2 different key-inputs, the hash function can generate the exact same index value.
How will we solve that ? This is called “collision”
Both of our existing structures can handle this situation.
Handling collisions depends on how we have structured our Hash table.
There are two ways to solve this
- Closed Addressing / Open Hashing
This technique is mostly used when Hash tables are implemented in a simple way where each bucket has only one ( key, value ) pair.

Linear Probing is the most common out of many “Closed Addressing / Open Hashing” techniques
- Linear probing
When a “Hash function” returns the same index number for two different key inputs, then if the existing bucket is already occupied by another (key, value) pair, for which the hash function generated the same index, we will find the next available empty bucket.
We will do a linear search until we find the next available bucket, it can be the immediate next bucket or can be found while traversing the hash table array elements linearly, starting the current index .
There are some other methods to solve collisions that involve “Closed Addressing / Open Hashing”. Some are mentioned below
- Quadratic Probing
- Double hashing
- Separate Chaining ( Open Addressing / Closed Hashing )
Our second way of implementing buckets, where each bucket can contain multiple ( key, value ) pairs, is a solution to handle collisions in a better way.
This is also called separate chaining. where multiple
( key, value) pairs are chained using an array or linked list.
Separate Chaining is most preferred.
Other than Closed Addressing and Open Addressing, we have
- Robin Hood Hashing
- Cuckoo Hashing
- 2-Choice Hashing
- Separate Hashing
How does Hashing work (in short ) ?
Hash Table Implementation with Linear Probing
class HashTable {
constructor() {
this.table = new Array(127); // Array size for hash table
this.size = 0;
}
_hash(key) {
let hash = 0;
for (let i = 0; i < key.length; i++) {
hash += key.charCodeAt(i);
}
return hash % this.table.length;
}
// Set key-value pair using linear probing for collision handling
set(key, value) {
const index = this._hash(key);
let currentIndex = index;
// Linear probing: find the next available slot if a collision occurs
while (this.table[currentIndex] && this.table[currentIndex][0] !== key) {
currentIndex = (currentIndex + 1) % this.table.length;
}
// Insert the key-value pair in the found slot
this.table[currentIndex] = [key, value];
this.size++;
}
// Get value associated with the key using linear probing
get(key) {
const index = this._hash(key);
let currentIndex = index;
// Linear probing: search for the key in the table
while (this.table[currentIndex]) {
if (this.table[currentIndex][0] === key) {
return this.table[currentIndex][1]; // Return the value if key is found
}
currentIndex = (currentIndex + 1) % this.table.length;
}
return undefined; // Return undefined if key is not found
}
// Remove key-value pair from the hash table using linear probing
remove(key) {
const index = this._hash(key);
let currentIndex = index;
// Linear probing: search for the key in the table
while (this.table[currentIndex]) {
if (this.table[currentIndex][0] === key) {
this.table[currentIndex] = undefined; // Remove the key-value pair
this.size--;
return true;
}
currentIndex = (currentIndex + 1) % this.table.length;
}
return false; // Return false if key is not found
}
// Display the hash table
display() {
this.table.forEach((values, index) => {
if (values) {
console.log(`${index}: [ ${values[0]}: ${values[1]} ]`);
}
});
}
}
// Example usage
const ht = new HashTable();
ht.set("France", 111);
ht.set("Spain", 150);
ht.set("ǻ", 192);
ht.display();
// Outputs something like:
// 83: [ France: 111 ]
// 84: [ Spain: 150 ]
// 85: [ ǻ: 192 ]
console.log(ht.size); // Outputs: 3
ht.remove("Spain");
ht.display();
// Outputs:
// 83: [ France: 111 ]
// 85: [ ǻ: 192 ]

Hash table implementation using Separate Chaining ( Array of Array )
class HashTable {
constructor() {
this.table = new Array(127); // Hash table with 127 slots
this.size = 0;
}
// Private method to generate a hash value based on the key
_hash(key) {
let hash = 0;
for (let i = 0; i < key.length; i++) {
hash += key.charCodeAt(i);
}
return hash % this.table.length; // Return index by applying modulo
}
// Method to add or update a key-value pair
set(key, value) {
const index = this._hash(key);
if (this.table[index]) {
// If there's already a bucket at this index, check for the key
for (let i = 0; i < this.table[index].length; i++) {
if (this.table[index][i][0] === key) {
this.table[index][i][1] = value; // Update value if key found
return;
}
}
// Key not found, so add new key-value pair
this.table[index].push([key, value]);
} else {
// If no bucket exists at this index, create a new one
this.table[index] = [];
this.table[index].push([key, value]);
}
this.size++; // Increase size of the hash table
}
// Method to retrieve a value by its key
get(key) {
const index = this._hash(key);
if (this.table[index]) {
// Check each key-value pair in the bucket
for (let i = 0; i < this.table[index].length; i++) {
if (this.table[index][i][0] === key) {
return this.table[index][i][1]; // Return value if key matches
}
}
}
return undefined; // Return undefined if key not found
}
// Method to remove a key-value pair by its key
remove(key) {
const index = this._hash(key);
if (this.table[index] && this.table[index].length) {
// Check each key-value pair in the bucket
for (let i = 0; i < this.table[index].length; i++) {
if (this.table[index][i][0] === key) {
this.table[index].splice(i, 1); // Remove the key-value pair
this.size--; // Decrease size of the hash table
return true;
}
}
}
return false; // Return false if key not found
}
// Method to display the contents of the hash table
display() {
this.table.forEach((values, index) => {
if (values) { // Only display if there's a bucket at this index
const chainedValues = values.map(
([key, value]) => `[ ${key}: ${value} ]`
);
console.log(`${index}: ${chainedValues.join(", ")}`);
}
});
}
}
// Testing the HashTable class
const ht = new HashTable();
ht.set("France", 111);
ht.set("Spain", 150);
ht.set("ǻ", 192);
ht.display();
// 83: [ France: 111 ]
// 126: [ Spain: 150 ], [ ǻ: 192 ]
console.log(ht.size); // 3
ht.remove("Spain");
ht.display();
// 83: [ France: 111 ]
// 126: [ ǻ: 192 ]
